scobility 🌶

What if block rating…didn’t matter?

I’ve been getting into D&D a lot lately so the urge to write “Tasha” here was overwhelming

problem statement

Over the last few years in the post-ITG score attack scene, it’s become somewhat painfully apparent that a single number doesn’t do a good job of summarizing the difficulty of a chart.

The single number attached to a chart is its “block rating”, or the number of blocks that the DDR song wheel fills in when you scroll over it. This also used to be known as “foot rating” back when DDR used a string of little feet instead of blocks.

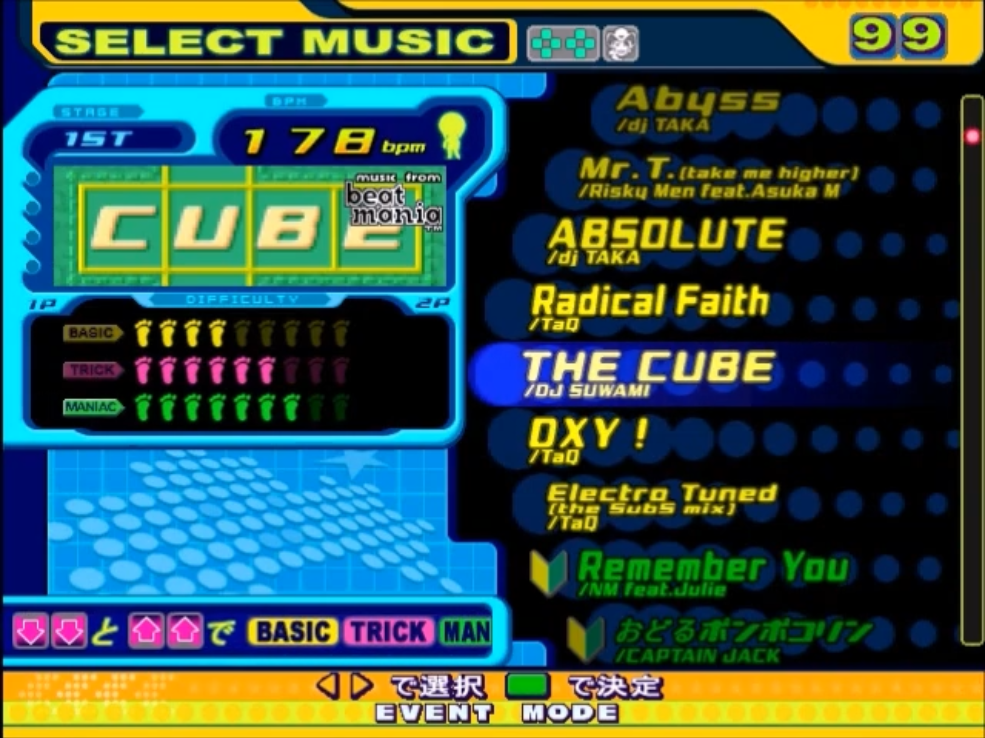
It’s generally agreed that this block rating is a measure of how hard it is for a player to survive the chart until the end – that is, the “passing difficulty.” A chart rated 9 could be extraordinarily complex or straightforward to a fault, but if your goal is simply to survive the chart, you can expect it to be comparable to other 9s (or “9-footers”).

Simfile artists and tournament organizers have tried various methods to give the player a little more warning about the complexity of a chart, relative to its plain block rating:

• Finer divisions of the block rating (e.g., a 12.9 will be much more difficult when compared to a 12.1)
• A secondary descriptive scale (e.g., a 12-D will be much more complex than a 12-A)
• A bunch of secondary descriptive scales that work together (DDR called it the “groove radar”; the score attack folks have a “tech radar”)
• Listing what’s actually in the chart (also known as “tech notations”)
• Capitulation

However, every rhythm game community loves to argue about difficulty ratings (it’s our FGC character matchups or maybe fantasy sports leagues). Why should tacking on an extra number or two change that? Now we have more numbers to discuss!

I think there’s value to having as consistent a rating scale as possible, but I also don’t like how all new simfile releases have come down to “bro this number is wrong…how could you assign the wrong number bro.” And I feel like part of the reason these discussions happen so much is the subjective origin of all the number choices. If a human picked it, the human could be wrong – or, at the very least, it is fertile ground for an opinion.

International Timing League and its very large dataset had me thinking, though. If enough people play the same set of charts, some sort of ordering should emerge – and maybe we can derive a scale that’s totally empirical, without per-chart human involvement? Since only passes were recorded for event purposes, I assumed that it wouldn’t say much about the passing difficulty, but the player’s-best score data is quite rich.

first forays

The concept of “scobility” started to materialize:

• Compare pairs of charts by listing which entrants played both and comparing their scores between the charts. Some sort of shape should materialize in the scatterplot, and the “harder” chart is the one the entrants are getting lower scores on.
• Fit an equation to this shape that will serve as a predictor: suppose a new entrant pops up with a score on chart A; by using this function, we should be able to approximate what their score on chart B should be.
• Assemble these pairwise relationships into some relatively monotonic ordering, and if there’s a compounding numeric parameter that falls out of the ordering, use that as the complexity rating or “spice level” of the chart.

I tossed the final ITL dataset into a jupyter notebook and started messing around, plotting chart scores against other charts’ scores and looking for patterns.

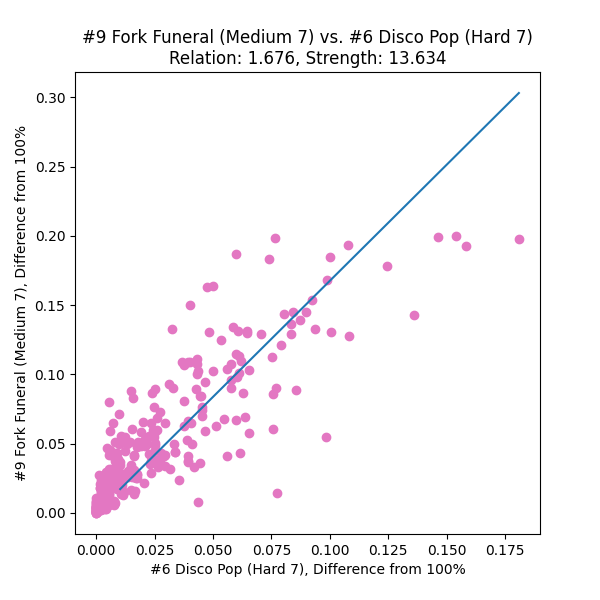
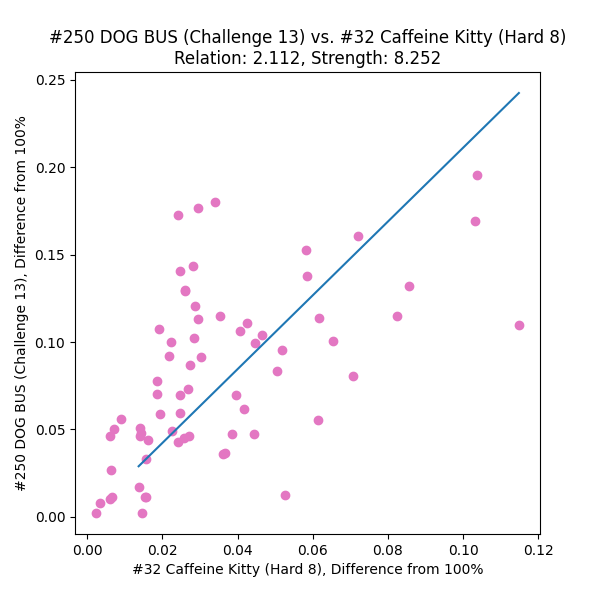
Armed with a few dozen chart relationship plots, I came to the conclusion that

• a plain ol’ linear best-fit through the (100%, 100%) point
• with scores under 80% (“struggling to pass” territory) discarded
• with scores over 99% (“you should move on” territory) discarded

might be enough to establish numeric relationships between charts.

spice level

For any* pair of charts in the ITL dataset, we now have a way to derive scores on one chart in terms of the other – and what’s more, it’s a single multiplicative coefficient per pair. How do we string together a reasonably monotonic ordering based on all these relationships?

I think the “right” approach here would be to construct a graph and minimize travel distances by removing direct links where a shorter hop-through exists. I started to code this up and then became Lazy™:

1. Derive the coefficient for each pair of charts in both directions.
2. Sort all (~10⁵, shush) of these relationships.
3. Throw out every ordered chart pair under 1×.
4. Starting from the closest pair to 1× and working upward, insert the involved charts (B vs. A) into a running list:
   • A walks along the line ascending until it finds the first already-placed chart, C, that loses to it (i.e., C vs. A has a coefficient less than 1×).
   • B does the opposite of all that (walks the line descending, looking for the first winning chart).
   • If either chart is already in the line, skip it.
5. Repeat until all* charts are in the running list.

In practice, when the neighbors in this list are each compared, this gets us almost all the way to fully monotonic – but it could be slightly better, there were 10~20 obviously misfiled charts at this stage. So I took a few iterations and bubble sorted any out-of-order pairs that could be improved by simply swapping their positions 😳

The ordering could still be better, though. Comparing neighboring charts makes for a reasonable first pass. If our view extends a few spots to either side, does the placement of each chart still seem sensible? At this point I began incorporating the strength of each relationship (based on the number of entrants in common).

1. Assign a provisional “spice value” of 1 to the first chart in the list.
2. Walk down the list in ascending order.
3. Multiply each chart’s provisional value by the coefficient with its next-door neighbor to get the next chart’s provisional value.

Once all charts have a provisional value, walk the list again:

1. Check the relationship each chart has with its neighbors a few spots up and down the list.
2. Multiply the neighbors’ spice values by the coefficient they share with the focus chart. (If the spice values are accurate, these products should all be the same!)
3. Take the weighted average, using the strength of each relationship as the weight. (Self-weight is determined by the number of people that played it.)
4. This average value will be retained as the result.

Charts can be re-organized by their new spice values, and this “windowed” neighborhood approach can be iterated as appropriate. A few swaps do happen in the first few iterations, but I was surprised to find that the ordering and values converge pretty strongly to a final arrangement after a few hundred iterations! (using a –10/+6 lopsided window, still fiddling with these values too…)

Now, the question of presentation…how do I express a “spice level”? Since it took a compounded multiplication to achieve each chart’s value, I don’t want to lose precision (or sow discouragement) in the low end, so I figured a logarithm of the raw spice content would be suitable.

By using log₂ of the raw spice value, I can set up a nice relationship: if a chart’s spice level increases by one, it is “twice as hard” to score on – for example, a 98% score on a 2.0辛 chart would be as powerful as a 96% score on a 3.0辛, or a 92% score on a 4.0辛.

And, without further data massaging, we have a “spice ranking” of all* the ITL charts!

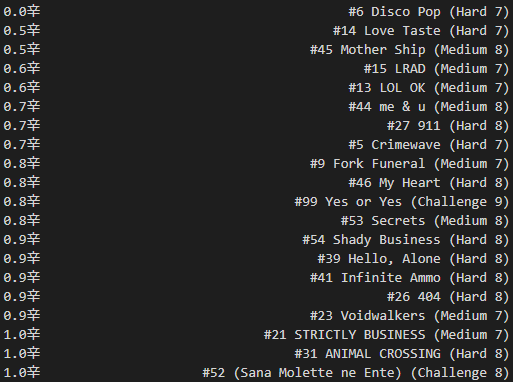
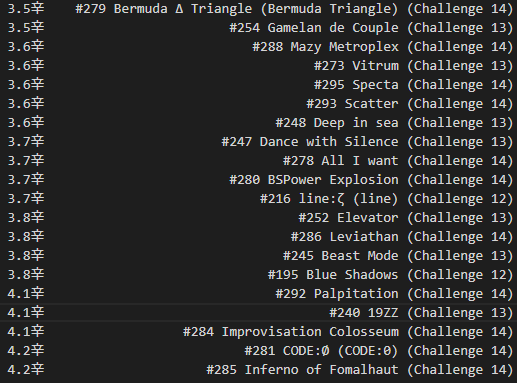
* Some charts just weren’t played by enough people (hello, Technological Transcendence full mix).

what’s in it for the player?

Applying the concept of spice level even further: it should be possible to look at a player’s scores and pick out the ones that are particularly good, or could be easily improved.

I was heavily influenced, even just to start this project, by ereter’s dp laboratory, which ranks IIDX double players and charts by their clearing strength, using (maybe) magic or (probably) something similar to what I’m inching towards here. A player summary and a skill analysis was always on the menu.

First, I needed a measure of each score’s quality. Because every increment of spice level represents a doubling of “lost dance points”, I needed to convert that quantity to a logarithmic representation as well.

• I subtracted each score from 100% (plus a tiny bit extra for asymptote avoidance) and took log₂. The better the score, the smaller this number.
• Then I anchored the value by running a score of 0% through the same formula and subtracting it.
• Finally, this quantity gets subtracted from the spice level to determine the score quality.

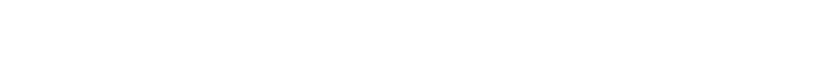
The expectation behind this quality calculation is that a perfectly consistent player should be able to get the same score quality on every chart. Due to skillset differences and the number of runbacks, this isn’t going to be exactly true, but it should hold pretty well. And the results were very encouraging:

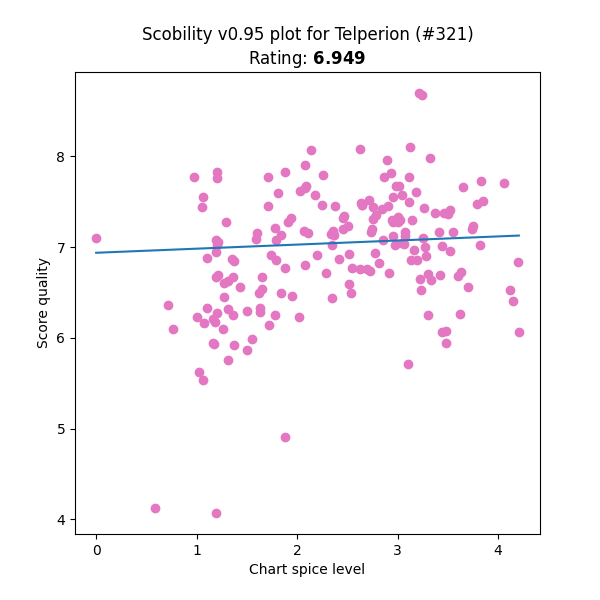
Not only that, but it’s very little extra work to:

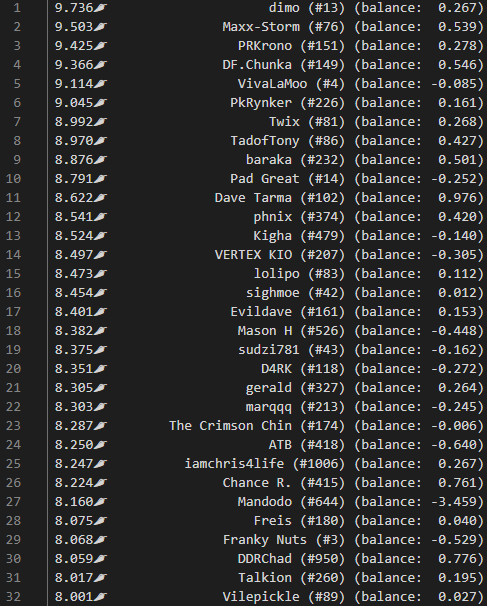
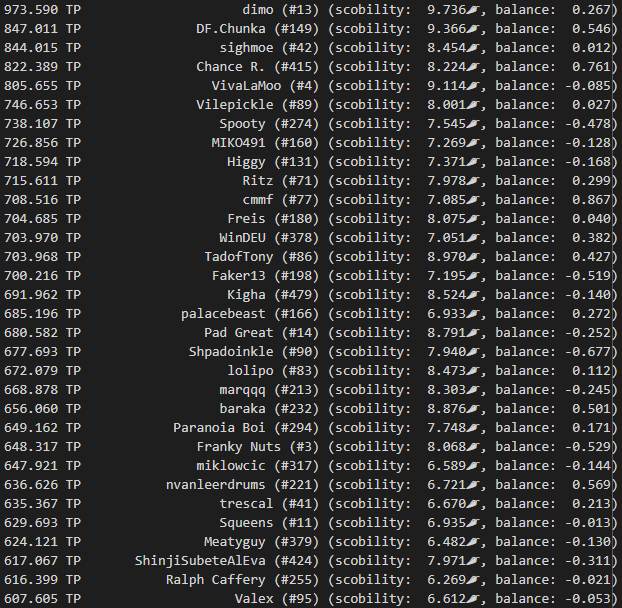
• Rank players based on this average scoring ability, or “scobility”
• Observe whether the player is stronger at “harder” or “easier” songs, by checking a trend line
• Ranking the quality of each player’s scores, and picking out:
  • The best 5, as standout scores
  • The worst 5, as improvement opportunities

If you were a reasonably active participant in ITL, you can have a look at what scobility thinks about you here. Curious whether you agree 🙂 Also, the source code is on github.

oh, and one more thing…

None of these calculations incorporate block rating!

Well, in some sense it does, because folks opted to play some songs and not others, looking for whatever particular challenge suited them. But I’m hoping that evened itself out pretty well.

Now if only we had something like this for passing difficulty… 🥸

appendix

I know you’re gonna ask about puns, but really, “scobility” = “score ability” because I love portmanteaus too. It’s also a nod to jubeat’s “jubility”, as well as the Scoville heat rating scale that inspired a lot of the aesthetic.

A few additional thoughts and/or disclosures:

• One major shortcoming of this method is that you need a sufficient number of players playing every song to run these calculations. There’s no way to assign a value to a chart just from looking at chart features, at least for now.
• Aggregate stats are hard. Simply averaging all score qualities for a player benefits people who only play songs they’re good at. It might be a better idea to calculate based on a player’s top 50 or something. Sounds familiar…
• I feel more comfortable using data from an event that put a lot of participants in a tourney mindset – I have more faith that folks put effort (and maybe multiple plays) into their scores, instead of half-hearted one-offs on charts they didn’t like, which would skew certain songs poorly.
  • The long term of the event might have some side effects of improvement, though – if an entrant made too many gains then maybe their score correlations will warp the results!
• Expressing spice level any more precisely than the tenths place probably isn’t worth it, due to all the fudge and kludge packed into the estimation process.
• There are a bunch of tunable parameters in this process that I’ve eyeballed or ballparked at most:
  • Score quality offset
  • Spice neighborhood window
  • Iterations of bubble sort and window sort
  • Number of required common players to establish a chart pair
  • Best-fit strategy (linear vs. ???, discarded data point cutoffs)
• How well will this process apply outside the Waterfall scoring scheme? Does the reduced granularity of old-school ITG (i.e., GrooveStats) pose problems?
  • Could we shoehorn the skillattack or 3icecream data into it?? I suspect the DDR “money score” system would just defeat any high quality SDGs…
• Spice level need not stay constant – in fact, it should be allowed to update as more scores accumulate, and shouldn’t be baked into chart files.
  • Tech-ni-cal-ly players could take an adversarial approach and grind down (or sandbag up) the spice level of some chart…
  • There’s also no real need to pre-calculate the spice level when considering a chart for event or tournament inclusion. Just run regular spice level updates, and once enough players have tried the chart, it will fold itself into the rankings 😎

shoutouts

• The ITL committees, especially VincentITG and teejusb for their insanely hard work getting the event up and running with this level of automation, enabling this kind of analysis.
• G_Wen for the daily data scrapes, saving me from doing an API deluge of my own.
• Various fellow players that helped me steer my trains of thought as I teased progress.
• Dancing with one’s hands in one’s pockets.